 |
Géométrie médiévale, tracés d’instruments
|
Les traités médiévaux d’origine occidentale sont quasiment dénués d’informations concrètes sur les réalités matérielles des instruments de musique comme sur leur pratique. La séparation très nette et déjà profondément enracinée dans la tradition entre les préoccupations d’ordre théorique (qui, seules semblent dignes d’être développées par écrit) et celles d’ordre pratique (dont on suppose que la transmission se fait par d’autres moyens) constitue un obstacle majeur à l’avancée des connaissances en organologie médiévale comme dans les autres domaines touchant l’Histoire des sciences et des techniques.
Le XIIIème siècle, que Jacques Le Goff qualifie de “siècle des corporations”[1] voit se développer d’une façon sans précédent l’architecture et les arts mécaniques en Europe. Alors que le clergé monopolise toute forme évoluée de culture, notamment écrite, Roland Bechmann[2] a analysé comment les autres formes de savoir se communiquent. En mettant en évidence l’usage, chez les gens de métier, de procédés mnémotechniques pour les figures géométriques complexes, il nous invite à penser que dans certains domaines d’investigation le texte n’est plus le document roi. Le non écrit - vestiges archéologiques, images, traditions orales - dilate le domaine de l’Histoire.
La conviction que le dessin des instruments de musique à cordes est régi dès le Moyen Age par des proportions donc par une logique géométrique interne, est une conviction qui s’acquiert in situ, à proximité de documents iconographiques “de qualité” par la simple comparaison à l’aide du compas des dimensions de chacune des parties principales de l’instrument. L’absence quasi totale d’instruments réels conservés nous contraint à exploiter au maximum leurs représentations dans la sculpture et la peinture de cette époque. Contrairement à une opinion très répandue, ce n’est pas à partir du XVème siècle que ces images d’instruments deviennent “réalistes” et plus ou moins “fiables”. La justesse de l’œil, l’habilité des peintres et des sculpteurs et la connaissance réelle de l’objet représenté n’ont pas d’époque de prédilection : de tous temps, ont cohabité des artistes plus ou moins talentueux. L’expérience montre que certaines sculptures, notamment celles des portails des grands édifices gothiques mais aussi certaines enluminures de manuscrits où l’œil du dessinateur s’avère particulièrement “aiguisé”, sont riches d’informations et supportent d’une façon surprenante des analyses organologiques et géométriques très poussées.
Tant qu’il n’est pas passé par le filtre de l’expérience analytique, il n’est pas facile d’identifier à coup sûr ce genre de documents parmi la prolifération d’images médiévales à thématique musicale. Cependant, ce critère de “qualité”, quelle que soit l’époque, semble pouvoir se résumer par la double dualité suivante:
représentation savante ou représentation rustique / instrument savant ou instrument rustique
et se formuler ainsi:
Est on en présence
- d’une représentation rustique d’un instrument savant ?
- d’une représentation rustique d’un instrument rustique ?
- d’une représentation savante d’un instrument rustique ?
- d’une représentation savante d’un instrument savant ?
Toutes les images ne peuvent donc prétendre au même usage documentaire. Si l’ensemble des représentations peut être pris en compte, notamment pour les calculs statistiques et les études de contexte ou de fonction musicale, ce sont évidemment les instruments répondant positivement à la dernière question qui seront l’objet privilégié d’analyses organologiques poussées.
Aucun tracé occidental d’instrument ne nous étant parvenu avant les années 1440[3] Il est fondamental de s’intéresser aux seules certitudes écrites à notre disposition concernant les méthodes médiévales de conception et de dessin des instruments.
Premiers témoignages provenant d’écrits “techniques” du monde arabe.
Contrairement aux occidentaux, les érudits arabes s’intéressent très tôt aux problèmes concrets de facture instrumentale. Al-Kindy (†874) puis Ikhwan al-Safa (Xème siècle) nous livrent des informations précises qui seront reprises et développées jusqu’au XVème siècle sur les proportions régissant le dessin du luth, la nature des bois utilisés, le nombre de boyaux ou de fils de soie constituant chacune des cordes ainsi que des considérations sur la régularité des épaisseurs[4]. Du point de vue de la conception de l’instrument, le problème y est déjà clairement décliné sur le mode des proportions simples de nombres entiers :
- la longueur du luth devrait être le double de sa largeur,
- la profondeur la moitié de sa largeur,
- le manche le quart de sa longueur,
- le point d’attaque des cordes se trouve au dixième de leur longueur
- il correspond à la plus grande largeur de l’instrument...
Une iconographie non négligeable parmi laquelle la fresque de pavement du VIIIème siècle provenant de Qasr al-Hayr al-Gharbì (Syrie) et conservée au Musée National de Damas comme les sculptures des coffrets d’ivoire datés de la fin du Xème siècle provenant d’al-Andalus et conservés au musée du Louvre donnent une idée suffisamment précise de l’allure de l’instrument pour pouvoir suivre les indications d’Al-Kindy. L’ensemble de l’instrument se construit de face et de profil dans un rectangle remarquable : le double carré. (Fig. 1)

|
Fig. 1. Les proportions du luth |
Fig. 2. Dessin de luth |
Fig. 3. Tracé géométrique définissant les proportions de la caisse du luth de Safì al-Dìn. |
Il faut attendre les années 1333-34, pour trouver dans le Kitab al-adwar de Safì al-Dìn ‘Abd al-Mu’min (†1294) un dessin “technique” de luth. Dans ce traité théorique, l’instrument représenté est visiblement tracé au compas (Figs. 2 et 3). L’ensemble de l’instrument s’inscrit toujours dans le double carré, sa longueur représentant le double de sa largeur. Mais on note un certain nombre de modifications comme l’apparition des rosaces circulaires et la présence d’un angle marqué à la jonction caisse-manche qui sont survenues un siècle auparavant, probablement en Andalousie autour de la cour d’Alphonse Le Sage et du formidable développement culturel et musical qu’il a su favoriser.
Ce changement apparemment anodin traduit en fait le passage de l’instrument monoxyle traditionnel[5] à un instrument composé de nombreuses petites pièces de bois de fine épaisseur collées entre elles: les côtes. La généralisation de cette nouvelle technique de construction s’explique par des raisons évidentes d’économie de matériau; il n’est donc pas étonnant qu’elle se soit imposée beaucoup plus tôt pour les luths à la caisse de résonance imposante, que pour les instruments à archet dont le volume intérieur est resté beaucoup plus réduit jusqu’à la Renaissance.[6]
Mais revenons au dessin de Safì al-Mu’min pour constater que le contour de la caisse de résonance, d’une construction claire, est simplement obtenu avec deux ouvertures de compas de rapport 1/2: le diamètre du premier cercle s’inscrivant dans le carré du bas, constituant le rayon des arcs latéraux. Cependant, le problème nouveau créé par l’assemblage entre la caisse et le manche a modifié certains rapports proportionnels de l’instrument :
|
|
Al Kindy, IXème siècle |
Safi al-Mumin, XIIIème siècle 1/2 1/2 5/8 3/8 4/5 |
On sait que, dès le XIIème siècle, certains ouvrages de savants arabes ordonnant et synthétisant les apports de l’Antiquité et de l’Inde furent traduits en Sicile et à Tolède; leur diffusion vers le nord fut accélérée après la prise de Constantinople par les croisés en 1204 et par la “croisade” contre les Albigeois qui mit en contact les Francs du Nord avec la civilisation méridionale enrichie par ses relations avec l’Espagne et les Etats musulmans de la péninsule. Cette vaste culture fut enseignée dans les universités arabes d’Espagne au XIème et au XIIème siècle, indistinctement aux étudiants musulmans, chrétiens et juifs. L’impact sur le monde chrétien de la diffusion de ces traductions va être considérable dans tous les domaines, notamment en géométrie et en mathématiques. Du point de vue des instruments, c’est aussi à partir de ce moment que le rebab et le luth vont se diffuser vers le nord et y être très rapidement adoptés.
Premier témoignage provenant d’un traité “technique” du monde occidental.
C’est en Hollande, au XVème siècle, qu’Henri Arnault de Zwolle a rédigé ses “Oeuvres théoriques”. Ce manuscrit conservé à la Bibliothèque Nationale de Paris[7] consacre une première partie à des considérations scientifiques et astronomiques avant de dédier une deuxième section à la musique. C’est dans cette dernière que l’on trouve une série de dessins “techniques” concernant les instruments à clavier, la harpe et le luth, accompagnés de textes en latin expliquant les tracés géométriques et commentant les phases successives de construction des différents instruments. Ce texte a été traduit en français par Le Cerf et Labande[8] et les passages concernant le luth ont été étudiés par Ian Harwood[9] (qui a reconstruit cet instrument), par Gerhard Christian Söhne,[10] puis par Kevin Coates.[11]
Les trois auteurs ont analysé le dessin simple et rigoureux - malgré certaines petites imprécisions du tracé probablement dues à la nature du support (le parchemin) - et ont remarqué la longueur inhabituelle du manche (la moitié de la longueur de corde vibrante) par rapport à ce que l’iconographie de la période nous enseigne (Fig. 4). Nous ne reviendrons pas ici sur ces problèmes qui ont déjà été traités, notre intérêt étant de comparer ce document au dessin de Safì al Mu’min, réalisé plus de deux siècles auparavant.

|
Fig. 4. Dessin de luth et commentaires.
Extrait des Œuvres Théoriques d'Henri Arnault de Zwolle. Manuscrit Latin n° 7295, B. N. Paris. (d'après K. Coates). |
Fig. 5. Superposition du dessin de Safi al-Din et de celui de Arnault de Zwolle.
|
Fig. 6. Superposition des shémas de construction géométrique
d'après le dessin de Safi al-Din et de celui de Arnault de Zwolle. |
La construction géométrique de la caisse d’harmonie des deux luths est identique... La grande rosace centrale (préférée en occident) a remplacé les deux roses latérales plus petites des instruments du sud. La partie supérieure du dessin de la table, à sa jonction avec le manche, plus étroit chez Arnault, s’est adoucie d’un arc supplémentaire. Mais les deux instruments, s’inscrivant dans une grande vesica piscis[12] sont régis par les mêmes proportions à l’exception du manche comme le montre simplement la superposition des deux tracés (Figs. 5 et 6).
Avant d’aller plus loin, nous devons revenir sur le fait que l’ensemble des dessins que nous venons d’évoquer sont régis par des proportions simples de nombres entiers. Si on se réfère à nouveau au petit tableau comparatif de la page 4, on constate que l’ensemble des proportions relevées sont des proportions... musicales.[13]
Le dessin d’al Kindy se construit avec les rapports 1/2, 2/3 et 3/4 : les intervalles harmoniques successifs des trois premières consonances principales que sont l’octave, la quinte et la quarte. Dans les desins plus tardifs, de Safì al Mu’min puis d’Arnault de Zwolle de nouvelles consonances apparaissent ; ce n’est plus la quinte (2/3) qui régit la proportion entre la longueur et la largeur de la caisse mais la tierce majeure (4/5). L’emplacement du chevalet, qui coïncide sur ces deux dessins, se situe d’après le texte d’Arnault à 1/6 de la longueur de la table[14] en partant du bas, soit la proportion de tierce mineure (5/6).
Bien qu’en aucun moment, Arnault ne se réfère explicitement à des proportions harmoniques ou musicales, tous les rapports proportionnels qu’il énonce peuvent s’y réduire sans exception:
- l’emplacement de la rose se situe au milieu de la distance séparant le chevalet du haut de la table[15] (octave);
- le diamètre de la rose est le tiers de la largeur de la table en cet endroit[16] soit les 2/3 pour la table (quinte);
- le manche, anormalement long pour l’époque mesure la moitié de la longueur vibrante[17] (octave);
- c’est le rapport 5/6 qui permet de situer la barre d’harmonie la plus proche du manche (tierce mineure);
- neuf côtes ou douelles sont nécessaires pour construire la caisse de l’instrument, c’est la proportion 8/9 qui définit le premier ton de la gamme...
De même, si on observe le dessin de Safì al Mu’min on peut constater que:
- le diamètre de chaque rose représente les 2/3 de chaque demie-largeur de la table (quinte);
- la longueur du chevalet correspond à moitié de la plus grande largeur de l’instrument (octave);
- la longueur de la caisse équivaut aux 5/8 de la longueur totale de l’instrument (sixte mineure).
Une vièle piriforme du début du XIIème siècle construite pour l’instrumentarium de Royaumont;
proposition de tracé géométrique
...Comme la solution ne se trouve pas sous forme de nombre, à l’aide de multiplications,
c’est par d’élégants tracés de lignes qu’elle s’obtient.Vitruve lib. VI. 3. [18]

Fig.7. Saint Castor et un ménestrel. Manuscrit Arundel 91, folio 218 verso, conservé au British Museum de Londres.
On est parfois saisi d’admiration devant certains dessins médiévaux par la justesse de l’œil, la maîtrise et la liberté de la main de l’artiste. L’ensemble de ces qualités se retrouvent notamment chez l’un des talentueux illustrateurs du manuscrit consacré à la vie des Saints compilé dans les années 1100-1120 probablement en Flandres. Ce passionnaire, conservé au British Museum de Londres sous la cote Ms. Arundel. 91, nous montre au folio 218 verso, (6 des ides de novembre), St. Castor et un ménestrel. Le Saint, qui tient une harpe dans chacune de ses deux mains a les pieds joints et les bras étendus de façon à former la lettrine “T” introduisant le texte: Temporibus quibus Dioclitianus perrexit pannonis... A sa droite, à plus petite échelle, on trouve un musicien jouant une vièle piriforme posée sur l’épaule (fig. 7). Le dessin de ce personnage est d’une grande pureté. Le trait libre et sûr dénote que son auteur était non seulement talentueux mais aussi expérimenté.
L’observation des contours de l’instrument, bien symétriques, aux lignes harmonieuses et à la tête élancée invite à vérifier la présence éventuelle de rapports proportionnels. Le compas montre simplement que la largeur de l’instrument constitue le tiers de sa longueur totale, les pointes du compas passant successivement le long de l’axe de symétrie, sur la baguette et sur le doigt de la main gauche appuyé sur la corde. La largeur de la tête représente la moitié de cette ouverture. La plus grande largeur de l’instrument se situe au quart de sa longueur... Bien qu’il soit peu probable, au vu de sa datation, que l’enlumineur de ce manuscrit aie pu avoir été en contact avec des ouvrages provenant du monde arabe, on ne peut s’empêcher de percevoir quelque similitude avec les énoncés d’Al Kindy et d’Arnault de Zwolle au sujet du luth. Une analyse géométrique plus poussée s’impose.
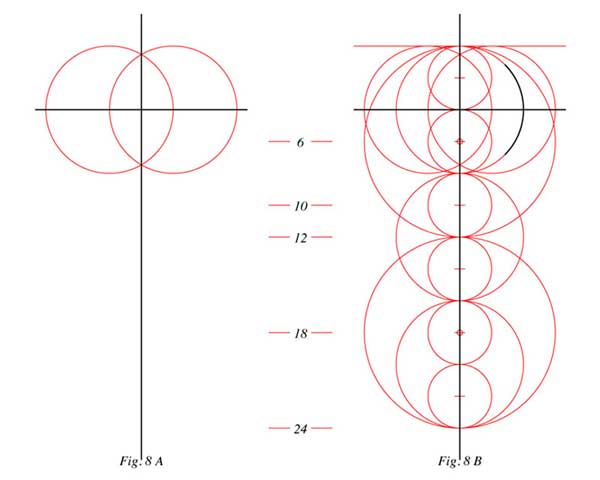
Fig. 8 A: Donnons au compas une ouverture de quatre pouces[19] et traçons un premier cercle. Avec la même ouverture, nous en traçons un deuxième en prenant pour centre un point quelconque du périmêtre du premier, le nouveau cercle passe par le centre du premier.
Cette figure simple, utilisée comme on l’a vu précédemment par Safì al Mu’min et Arnault de Zwolle pour le luth mais aussi par Villard de Honnecourt[20] est communément appelée Vesica Piscis. Constituée de la rencontre de deux cercles égaux, elle génère directement une myriade de constructions comme le triangle équilatéral, le carré, le pentagone, l’hexagone, le dodécagone ainsi que la racine de trois et les rectangles dorés.[21]
Soucieux de nous en tenir à la notion de géométrie purement pratique et sachant que les constructeurs médiévaux semblent avoir préféré les rapports et les formes géométriques les plus simples, nous n’allons utiliser la vesica que pour deux de ses propriétés élémentaires.
D’abord, elle va nous permettre de tracer la croix comme l’illustre la figure mnémotechnique des flamants chez Villard[22]. Ainsi, la vesica se substitue avantageusement à l’équerre dont Vitruve dit que “les artisans qui la fabriquent laborieusement, peuvent difficilement parvenir à rendre exacte”.[23]
A partir de ce moment l’espace est coordonné en deux dimensions. La deuxième propriété élémentaire est développée dans le dessin suivant.
Fig. 8 B: Sachant d’une part qu’avec un compas, il est plus facile de multiplier que de diviser mais sachant d’autre part que les multiplications répétées à l’aide ce cet outil sont souvent une source d’imprécisions, nous considérons les divisions créées sur l’axe horizontal par les intersections des deux cercles soit : 2, 4, 6, 8 et 12 pouces. L’écart de 10 pouces est donné par l’intersection de l’axe horizontal avec un troisième cercle de même diamètre que les deux précédents, obtenu en plaçant la pointe du compas au centre de la croix.
Les divisions de l’axe horizontal sont rapportées au compas sur l’axe vertical qui est celui de l’instrument. Tous les points de repères sont en place pour un instrument de deux pieds de long soit 24 pouces. Le diamètre de chacun des cercles de la vésica (8 pouces), est en relation de quinte par rapport à la longueur totale.
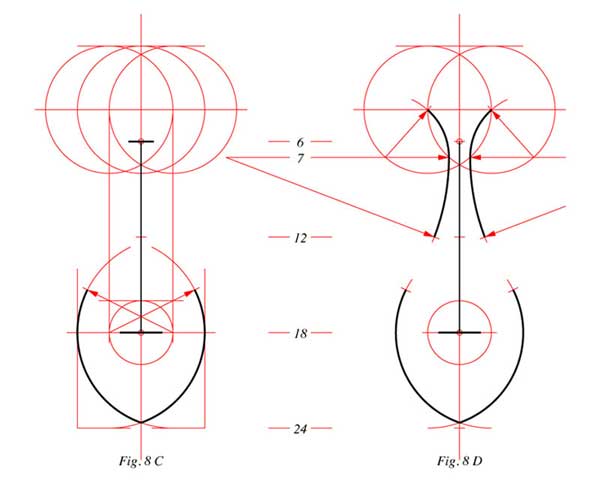
Fig. 8 C: Sur l’axe vertical, les points de quarte 6 et 18 représentent respectivement le sillet et le chevalet et déterminent une longueur vibrante d’un pied soit l’octave de la longueur totale de l’instrument.
D’après l’enluminure on sait que la plus grande largeur de l’instrument est le tiers de sa longueur, donc sa quinte, 8 pouces et qu’elle se situe au quart inférieur de sa longueur, au point de quarte 18, dans le même axe que le chevalet. Le dessin de la partie inférieure de la caisse de résonance s’obtient avec une ouverture de quarte, 6 pouces, en plaçant la pointe du compas sur chacun des points de quarte de cet axe transversal.
Fig. 8 D: On trace une perpendiculaire à l’axe vertical au point 7, son intersection avec les deux cercles de la Vesica détermine le centre de deux arcs de même rayon (4 pouces) qui dessinent la moitié inférieure de la tête. La pointe du compas vient alors sur cette même perpendiculaire pour tracer, avec une ouverture d’une octave (12 pouces) les deux côtés du manche.
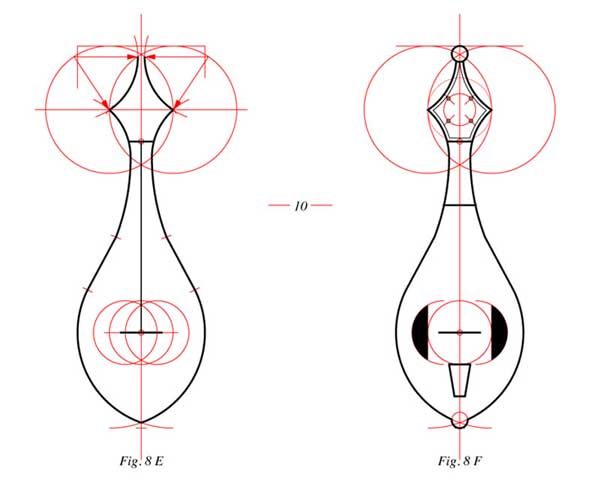
Fig. 8 E: Deux segments de droites (tangeantes) complètent la figure en reliant, de chaque côté de l’axe de symétrie, les arcs qui constituent le manche et la caisse.
A la pointe supérieure de la vesica, on trace une dernière perpendiculaire à l’axe vertical; celle-ci détermine, aux points d’intersection avec les deux cercles, les centres théoriques des deux arcs (toujours de rayon 4) qui permettent d’achever le dessin. Pour que le petit cercle couronnant l’édifice reste solidaire de l’instrument, on les décentre légèrement vers l’extérieur.
Une nouvelle vesica permet de tracer les ouies.
Fig. 8 F: L’extrémité inférieure de la touche située au point 10 détermine le point de quinte de la longueur vibrante des cordes. L’ensemble de l’instrument s’obtient avec trois ouvertures de compas correspondant aux consonances parfaites: octave, quinte et quarte.
|
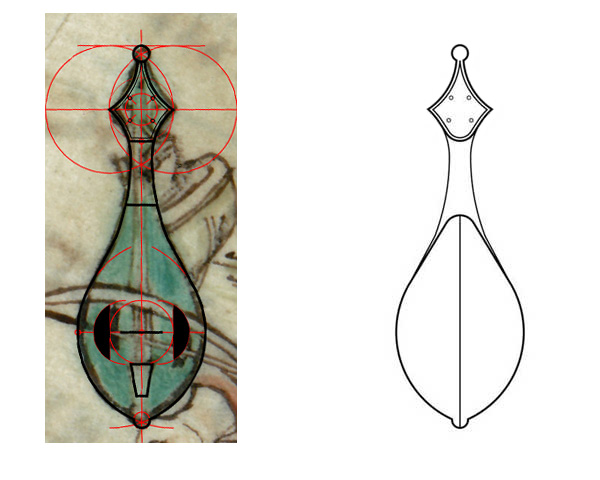
Fig. 9: Superposition du tracé obtenu et du détail
de la vièle piriforme du Manuscrit Arundel. |
Fig. 10:
Propositon pour une vue de dos. |
Commentaires.
On sait les liens indissolubles qui unissent la musique à la géométrie. Les instruments de musique étaient-ils soumis aux mêmes lois harmoniques d’intervalles et de consonances que la musique qui les a générés?
L’interprétation que nous avons donnée des documents iconographiques et du texte d’Arnault de Zwolle nous pousse à le penser. Mais aucune confirmation écrite explicite émanant de l’occident médiéval ne nous permet de l’affirmer avec certitude. A ma connaissance, il faut attendre encore deux siècles pour trouver dans les traités ce discours clairement énoncé.
C’est Marin Mersenne en 1624 qui, parlant du luth de son époque énonce clairement le problème en termes de proportions harmoniques “le manche ou la touche doivent être de même longueur que l’intervalle qui est depuis le commencement de la table jusqu’au milieu de la rose: c’est à dire que le manche doit avoir cinq parties et la table huit, afin qu’elle fasse la proportion de la sexte mineure avec le dit manche et qu’il ne se rencontre rien dans le luth qui ne soit harmonique”[24] . Plus loin, alors qu’il se dispense de nous décrire la basse de violon (en regard de la qualité de la gravure) il tient tout de même à préciser que la longueur du manche est le tiers de la longueur de la table.[25]
Cette même façon de concevoir les instruments est abondamment développée par Pablo Nassare dans un traité dont le quatrième livre, entièrement dédié aux proportions harmoniques, s’adresse aux facteurs d’instruments de son temps.[26]
Dans le chapitre XIV qui traite des ‘dimensiones” , il énonce: “La longueur est selon le corps de l’instrument, la largeur et la profondeur doivent être selon les proportions sonores, en proportionnant la longueur avec la largeur, la largeur avec la profondeur, en observant que toutes ces proportions soient de celles qui constituent des consonances; il doit en être ainsi pour que les voix de l’instrument soient claires et délectables. L’expérience enseigne, que tout corps creux qui est en proportions sonores, résulte de meilleure sonorité, que celui qui ne l’est pas”[27]
Après avoir constaté que cette loi régissait également les proportions intérieures des édifices religieux, Nassarre décrit dans le chapitre suivant[28] les “proportions sonores” qui doivent être respectées pour construire les instruments. A la page 462, après quelques considérations générales au sujet des vihuelas et des guitares il résume: “ La longueur de la caisse doit être le double de sa plus grande largeur[29] (“proporción dupla”), la plus petite largeur doit être les quatre cinquièmes de la plus grande (“proporción sexquiquarta”, la partie centrale la plus étroite le tiers de la longueur (“proporción tripla”) . C’est en prenant les deux-cinquièmes de chacune des deux plus grandes largeurs que l’on obtient les profondeurs d’éclisses au tasseau du haut et au tasseau du bas (“proporción dupla sexquialtiera”). Les mêmes proportions sont décrites plus loin et sont appliquées cette fois aux instruments de la famille du violon.[30]
Mais, Nassarre qui se réfère sans cesse dans le texte aux Anciens semble ignorer, en 1723-24, l’Harmonie Universelle pourtant publiée à Paris depuis presqu’un siècle. Déjà, en 1636, Marin Mersenne n’avait-il pas titré la proposition XXXVI de son livre premier : ” Démontrer que la plus agréable et la meilleure division des Consonances n’est pas Harmonique comme l’on a cru jusques à maintenant, mais qu’elle est Arithmétique : et que la division Arithmétique est cause de la douceur des dites Consonances”.
[1] LE GOFF (Jacques), Les intellectuels au Moyen Age, Paris : Seuil, 1957, p.73.
[2] BECHMANN (Roland), Villard de Honnecourt. La pensée technique au XIIIème siècle et sa communication, Paris : Picard, 1993, p. 305 et ss.
[3] Henri Arnaud de Zwolle, Oeuvres Théoriques, Ms. Lat. 7295, Bibl. Nat. de Paris.
[4] La grande majorité de ces textes a été publiée par FARMER (Henry Georges), Studies in Oriental Music. Londres : Harold Reeves, 1931, tome II. pp. 109-110 et 226-229.
[5] RAULT (Christian), “L’évolution du dessin des cordophones du XIème au XIIIème siècles révélatrice de l’évolution de leurs procédés de construction”, in: Musique Ancienne n° 22, Bourg La Reine: 1987, pp. 28-42.
[6] C’est à partir du début du XVIème siècle, alors que la taille des instruments à archet augmente que l’ancienne technique monoxyle sera progressivement abandonnée. Voir : RAULT (Christian), “Les modifications structurelles radicales des instruments à cordes au XVIème siècle”, in : Pastel n° 21, Toulouse : sept. 1994, pp. 30-36.
[7] Henri Arnault de Zwolle, Oeuvres Théoriques, Ms. Lat. 7295, Bibl. Nat. de Paris.
[8] LE CERF (G.) et LABANDE (E.R.), Les instruments de musique du XVème siècle, Paris, 1932. Dans cette édition fac-similé du manuscrit, l’intégralité du texte est traduit en français.
[9] HARWOOD (Ian), “A fifteenth-century lute design”, in : Lute Society Journal, Dublin : Dolmen Press, Vol. II,1961, pp. 3-9.
[10] SÖHNE (Gerhard Christian), “La géométrie du luth”, in : Musique Ancienne n° 14, Bourg La Reine : C.A.E.L., juin 1982, pp. 4-8.
[11] COATES Kevin, Geometry, proportion and the art of lutherie, Oxford : Clarendon Press, 1985, pp.18-19.
[12] Voir note : 20.
[13] La seule proportion indiquée par ces auteurs qui ne corresponde pas à un intervalle harmonique n’est pas destinée au facteur d’instruments mais au musicien : il s’agit du point optimal d’attaque du plectre par rapport à la longueur de la corde : 1/10.
[14] Item stephanus stabit in sexta parte todius longitudinis...
[15] Item centrum fenestre stabit in medio inter stephanum et caput totius corporis secluso collo...
[16] Et per dictum centrum ex traverso trahatur linea que si dividatur in 3 partes una illarum partium denotat dyametrum fenestre...
[17] Ce manche est d’ailleurs si long qu’Arnault constate simplement que la place manque pour le dessiner en entier : Item collum debet habere longitudinem linee iK usque ad stephanum superiorem sed hic nimis est breve propter papirum...
[18] VITRUVIUS Pollio, De archiectura libri decem, Paris: Panckoukr, traduction Maufras, 1847, lib. VI. 3. (Texte concernant la duplication du carré).
[19] Unité de mesure pouvant varier suivant les époques et les régions de 2,5 à 3,1 voire 3,4 cm. Il y a 12 pouces dans un pied, le pied du roi ou pied de Paris (très proche de celui utilisé pour la construction de Saint Denis) correspond à 32,484 cm soit un pouce de 2,707 cm.
[20] “Comment tracer trois arcs différents avec la même ouverture de compas” dessin du folio 21 recto du manuscrit de Villard commenté par BECHMANN Roland: Les dessins techniques du Carnet de Villard de Honnecourt in: Carnet de Villard de Honnecourt, XIIIème s. Introduction de Alain Erlande-Brandebourg et commentaires de Régine Pernoud, Jean Gimpel, Roland Bechmann, Paris : Stock, 1986, p. 42.
[21] COATES Kevin, Geometry, proportion and the art of lutherie, Oxford : Clarendon Press, 1985, pp.18-19.
[22] BECHMANN (Roland), Villard de Honnecourt. La pensée technique au XIIIème siècle et sa communication, Paris: Picard, 1993, p. 320.
[23] VITRUVIUS Pollio, idem, lib. IX, pp. 313-315 : “Quam magno labore fabri normam facientes vix ad verum perdicere possunt”
[24] Marin MERSENNE, Harmonie Universelle, Paris, 1636, éd. facsimilé du CNRS, Paris 1965, Tome III, Livre second, proposition II, p.50.
[25] Ibid. Tome III, Livre Quatrième, proposition IIII, p.185.
[26] NASSARRE Pablo, Escuela Musica, segun la practica moderna, Saragosse, 1723, éd. facsimilé de l’Institution “Fernando el Catolico” (C.S.I.C.), Saragosse, 1980.
[27] ”La longitud a de ser segun el cuerpo del instrumento, la latitud y profondidad han de ser segun proporciones sonoras; proporcionando la longitud con la latitud con la profundidad, observando el que todas estas proporciones sean aquellas que constituyen consonancias; pues conviene assi para que las vozes del instrumento sean claras y deleytables. La experiencia enseña, que todo concavo que esta en proporciones sonoras resulta de mayor sonoridad que el que no esta.”
[28] “Des proportions que doivent observer les artisans dans la construction des harpes, vihuelas, guitares, et tout instrument à archet”.
[29] Noter au passage que l’on retrouve la figure du rectangle remarquable: double carré, mais cette fois ci, c’est seulement la caisse de résonance qui s’y inscrit et non plus l’ensemble de l’instrument. (Cette remarque recoupe une observation de Francisco Luengo (note n°8 de sa communication), sur le dessin des instruments post-renaissance et s’explique très simplement par l’évolution des procédés de construction). Sur ce sujet voir: RAULT Christian, “Les modifications structurelles radicales des instruments à cordes au XVIème siècle, in: la revue Pastel n° 21, sept. 1994, pp.30-36, et du même auteur: ”Iconographie et reconstitution, quelques expériences récentes et une illustration: la vièle ovale”, in: Les cahiers de musique médiévale n° 2: Des instruments pour les musiques du Moyen Age, Paris: Centre de Musique Médiévale de Paris, 1997,pp.28-43.
[30] A l’exception des hauteurs d’éclisses qui passent de 2/5 à 1/5 des plus grandes largeurs.